Raccordement de lignes de chemin de fer

• Problème original
• Méthode alternative
• Analyse et Utilisation en classe

Illustrations de cet article (source).

Problème original

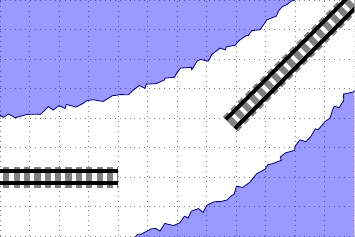
L'étude du raccordement de deux lignes de chemin de fer est un problème classique en première, dans le chapitre sur les dérivées. La méthode généralement attendue est de déterminer l'équation d'une fonction dont les tangentes à la courbe, aux points de raccordement avec les deux demi-droites, sont ces mêmes demi-droites. J'utilise, comme exemple concret pour illustrer les contraintes que le tracé d'une ligne de chemin de fer doit respecter, la ligne de chemin de fer menant à Quiberon (en projetant la carte avec OpenStreetMap, pour montrer qu'il existe des alternatives à Google).

Pour une description détaillée d'une telle séquence, voir par exemple l'article de Fabien Aoustin, Des maths sur les rails ?¹.

Cette solution n'est pas la solution utilisée en réalité (si je ne fais pas d'erreur ; je ne suis pas spécialiste), car le rayon de courbure change de manière discontinue, ce qui entraîne divers problèmes. La courbe qui convient est la clothoïde, mais elle est hors de portée de cet article.

Méthode alternative

Après avoir utilisé cette activité lors du chapitre sur les dérivée, j'ai pensé à une solution alternative, utilisant les vecteurs et les équations cartésiennes.

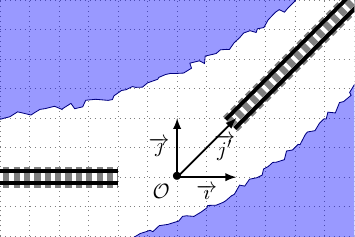
Au lieu de prendre un repère orthonormé $\left(O, \overrightarrow{\imath}, \overrightarrow{\jmath}\right)$, utilisons le repère ni orthogonal ni normé $\left(O, \overrightarrow{\imath}, \overrightarrow{j'}\right)$ représenté ci-dessous.

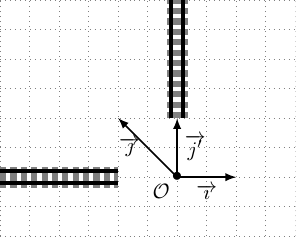
Je ne suis pas habitué à manipuler de tels repères. Représentons notre problème en faisant comme si le repère $\left(O, \overrightarrow{\imath}, \overrightarrow{j'}\right)$ était orthonormé. Nous obtenons alors la représentation suivante.

Dans cette représentation, une courbe qui convient (telle que les tangentes aux points de raccordement sont les demi-droites correspondant aux lignes de chemin de fer déjà placées) est un quart du cercle de centre $I\left(-1, 1\right)$ et de rayon 1. Les élèves sont alors capables de montrer qu'une équation cartésienne de cette courbe est $(x+1)^2+(y-1)^2=1$ (cette équation décrit le cercle complet, plutôt que le quart de cercle utile).

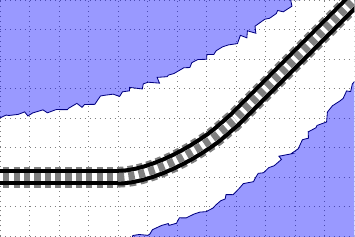
Reste alors à effectuer un changement de repère pour obtenir l'équation du quart de cercle intéressant, dans le repère orthonormé $\left(O, \overrightarrow{\imath}, \overrightarrow{\jmath}\right)$, Cette équation est la suivante, et sa représentation graphique est représentée en dessous. $$ \left\{\begin{array}{l} x=t+1-\sqrt{1-(t+1)^2}\\ y=1-\sqrt{1-(t+1)^2} \end{array}\right. \text{pour $t\in[-1;0]$.} $$

Analyse et Utilisation en classe

La solution trouvée n'est, à mon avis, ni meilleure ni moins bonne que celle décrite en début d'article (la courbe d'un polynôme de degré 2 peut convenir ici). La démarche est par contre plus complexe.

Je n'ai pas réalisé cette activité en classe, car j'ai trouvé cela trop technique :

• il faut « extraire » de l'équation de cercle l'équation du quart de cercle, en jouant avec les signes ;
• il y a un changement de repère, qui peut être un exercice intéressant, mais qui n'est pas au programme (donc qu'il n'est pas nécessaire de faire). Et j'avoue que moi-même je me suis emmêlé les pinceaux pour le réaliser ; j'ai donc peur que beaucoup d'élèves soient perdus ;
• la courbe trouvée est paramétrée, ce qui n'est pas au programme de première. Faire intervenir ceci à la fin d'une telle activité ne me paraît pas le meilleur moment pour introduire cette notion.

Peut-être que cette activité aurait davantage sa place en terminale ?

Néanmoins, si un collègue arrivait à faire quelque chose de cette activité, j'en serai ravi, et je serai curieux de savoir comment !